流程化编程思想在数学建模课程中的应用

流程化编程思想在数学建模课程中的应用

刘 冬 李雅婷 赵家浩 欧锦凤 贺超超

天津商业大学理学院 天津 300134

[摘要]：数学建模课程的优化理论，排队论，回归模型和模拟建模都需要借助数学软件来实现，从理论模型到软件实现的过程，需要学生具备扎实的编程能力和抽象思维方式。本论文通过数学建模课程的具体实例“蒙提霍尔问题”和“牛顿迭代”，来阐述流程化编程方法和授课思路，以及图形化的教学方法，使学生更容易理解流程，掌握建模理论，编写程序，提高学生处理实际建模问题的能力。

[关键词] 数学建模；流程化编程；图形化

[项目编号]JDS958 [项目名称]伴你学数统——大数据和统计学结合的创新应用实践

信息时代背景下，数学建模课程教师不仅应讲授建模理论，也应着重培养学生的程序编写和数学计算能力。数学建模课程的诸多重要章节：模拟建模，优化建模，排队论和回归模型都涉及到了程序编写问题：学生需要将理论模型通过数学软件实现并求解，这个过程需要学生具备扎实的理论功底和编程能力。同时，程序的编写需要创造性，这个过程也能提高学生的参与感和成就感。

对于编程初学者，教学的难点在于“程序的抽象化”，导致无从下手。在具体数学建模编程教学中，把抽象的理论流程化，图形化，具体化，从小处着手，按流程步骤实施程序编写，能加深学生对相关建模理论的理解，循序渐进完成模型求解，达到良好的教学效果 。

我们以数学建模课程中的具体实例来阐述流程化编程思想。

一、“蒙提·霍尔问题”

该问题出自美国的电视游戏节目“Let's Make a Deal”，名字来自该节目的主持人蒙提·霍尔。一名参赛者将看见三扇关闭的门（门的编号为1,2,3），其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定一扇门，但未去开启它的时候，节目主持人会开启剩下两扇门的其中一扇，露出其中一只山羊。然后，主持人会问参赛者要不要变更第一次的选择，而选择换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机会率 ？

讲解本题时，教师在现场找一位学生模拟几次这个游戏，这样游戏的规则就清楚了。然后，列出游戏中用到的各个变量，如下表：

表1：蒙提霍尔问题的变量列表

注意，我们考虑如下的情形：每次模拟，总假设参赛者会换门，然后考虑他是否中奖。模拟的流程图如图1所示。

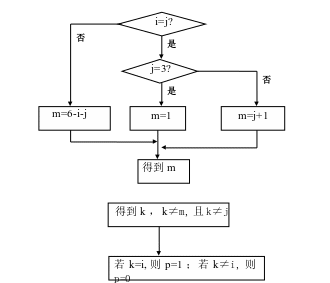
图1：单次蒙提霍尔问题的流程图

采用流程图展示程序结构有很多优点：问题结构清晰可见；程序编制过程形象具体；画出流程图后，每次只需考虑单独一步的程序编写，整合后就能把全部程序编写完成。

流程图的要点：

（1）第一步：如果i=j，即参赛者第一次就猜对了，那么主持人总是选择临近j的下一个门打开，这是不影响最终结果的。特别的，若i=j=3，那么主持人会揭开第1个门，即m=1；

（2）第一步：如果i≠j，即参赛者第一次没有猜对，则主持人此时的选择：主持人既不能揭开第i门，也不能揭开第j门，此时m≠i，m≠j，而三个整数m，i，j恰好是1，2,3的一个组合，即m+i+j=6,则m=6-i-j；

（3）确定了m后，由于假定单次模拟参赛者每次都更改最初的选择j，故参赛者最后的选择k≠j，而且k≠m，三个整数k，j，m恰好是1，2,3的一个组合，即k+j+m=6,则k=6-j-m；

（4）得到了参赛者最后的选择k，比较k与奖品位置i，即得p（是否中奖）。

在具体的授课过程中，教师首先提示学生总览模拟流程全局，明确编程目的；然后理解流程的每一步，并编写代码实现各步流程。特别的，我们可以很自然的引入程序的基本结构：分支结构和循环结构。个别变量可能取多个值，那么应采用分支结构处理；模拟过程需要重复进行，则应采用循环结构处理，对于本问题，循环模拟一万次，最后统计一万次模拟的实际中奖次数，就得到了对应策略的中奖概率。

在流程图讲解完毕后，对照流程图现场编写程序即可。下面是R代码实现的模拟流程。

#蒙提霍尔问题

#程序a模拟一次游戏

a=function(){

i=sample(1:3,1) #奖品位置i是取值1,2,3的随机变量

j=sample(1:3,1)

if(i==j){m=j+1

if(j==3){m=1}

}else{m=6-i-j} #分支结构确定m的取值

k=6-m-j #确定k的取值

if(k==i) p=1 else p=0 #确定p的取值

p

}

t=0 #调用a函数，模拟一万次游戏，t记录成功的总数

for(p in 1:10000){

t=t+a()

}

t/10000 #一万次游戏共中奖t次，中奖概率约为t/10000

二、牛顿迭代算法

数学建模的核心问题是研究函数和函数的极值，在优化理论中，牛顿迭代算法是求函数极值最基本的算法。理解牛顿迭代，使用数学软件实现理论是优化建模课程的基本要求。

我们以多元优化问题为例，考虑二元函数 在定义域上的最大值 ：

图像如下：

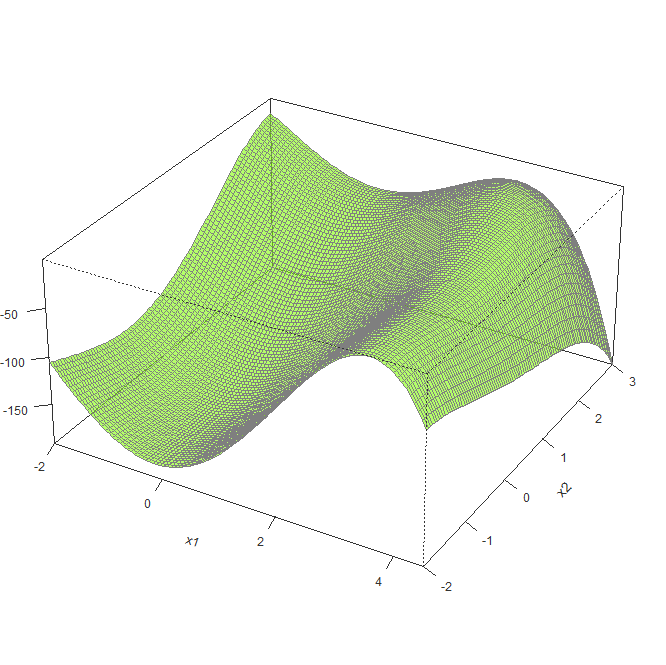
图2：二元函数的三维图像

牛顿迭代就是随机确定初始“登山点”： ，通过确定方向 得到下一个“登山点”： ，以此类推。注意，每步移动的步长为1。讲解时，重点对迭代项 进行说明，该方向指向山顶（函数最大值）。同时，我们发现，初始登山点的选取会影响迭代的效果。

理论上， 导函数形式简单但驻点不可求，故采用牛顿迭代寻求数值最优解，由牛顿迭代，若已知第 步最优点为 ，则迭代公式为

(1)

上述迭代算法的实现，还需考虑迭代的结束条件，存在两种结束条件：

1.如果 小于预先给定的常数 ，则迭代结束；

2.人为规定迭代次数为50次。

设定初始点 ，根据迭代算法公式（1），即可进行程序编写，最后的迭代路径如图3所示，明显可见，牛顿迭代在第一步就指向山顶方向，这既是牛顿迭代的优点：初始收敛速度快；也是牛顿迭代的缺点：临近山顶时收敛速度迅速变慢。算法可能会收敛到局部最优，而无法收敛到全局最优。

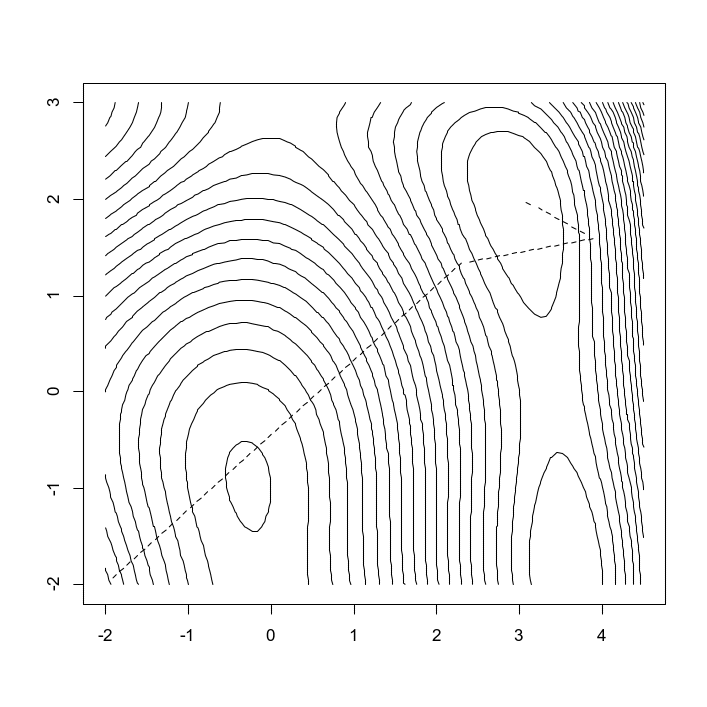
图3：寻找函数最优点的迭代路径示意图

三、总结

在数学建模课程上，教师讲解建模理论的同时，也应当结合数学软件实现理论。本文通过建模课程的具体实际问题，阐述了流程化编程思想和图形化理论展示，二者能够将晦涩难解的建模理论形象化，步骤化，使教学效果事半功倍。同时，学生在建模编程的过程中，能够提高逻辑思维能力和动手能力，从而收获参与感和成就感，明确数学建模的目的和意义，形成良性的学习路径。

[参考文献]

[1] Ross.Simulation[M],Elsevier Pte Ltd, 2013.

[2] Frank R,Giordano. A First Corse in Mathematical Modeling, Fifth Edition[M]. Brooks/Cole, 2014.

[3] Gentle, James E. Computational Statistics[M], Springer, 2009.

[4] 茆诗松,程依明.概率论与数理统计[M].北京,高等教育出版社,2011.

刘冬 邮箱：lxyld@tjcu.edu.cn

通讯地址：天津市北辰区天津商业大学理学院 300134